Pre záujemcov dávam k dispozícii slajdy z mojej habilitačnej prednášky z 27. mája.

Na prvý pohľad to je poriadna hlúposť. Ale taký päťuholník existuje. A nielen päťuholník. Keď sa s nimi chceme stretnúť, musíme zmeniť prostredie, kde ich konštruujeme. Musíme opustiť svet euklidovskej geometrie a vojsť do sveta tej neeuklidovskej, v našom prípade hyperbolickej geometrie.

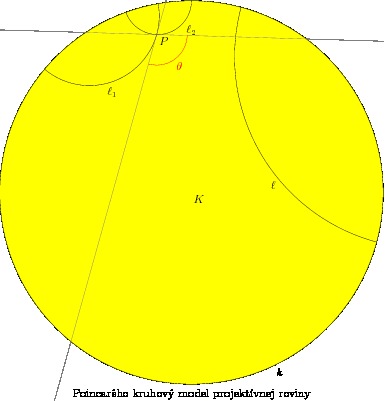
Jedným z modelov takejto roviny je Poincarého kruhový model hyperbolickej roviny. Je daný kruhom K v euklidovskej rovine (tej, na ktorú sme zvyknutý), z ktorého vynecháme hraničnú kružnicu k. Takúto množinu nazývame aj otvoreným kruhom. Bodom v takejto rovine je každý bod otvoreného kruhu. Priamky sú dvojaké. Jednak všetky priemery daného kruhu (samozrejme bez bodov ležiacich na hraničnej kružnici k) a jednak časti kružníc, ktoré sa s hraničnou kružnicou pretínajú pod pravým uhlom a ležia vo vnútri otvoreného kruhu. Uhol Θ dvoch takýchto priamok hyperbolickej roviny (teda častí euklidovských kružníc) sa určuje ako uhol dvoch euklidovských priamok, ktoré sú dotyčnicami ku kružniciam určujúcim priamky hyperbolickej roviny v ich spoločnom bode vnútri kruhu K. Asi dosť komplikované na prvý pohľad, ale obrázok všetko vyjasní.

V euklidovskej rovine sa ku každej priamke l a bodu P mimo nej dá zostrojiť jediná rovnobežka q (t.j. priamka q, ktorá nemá s tou pôvodnou spoločný žiaden bod a obsahuje bod A). V neeuklidovskej geometrii to neplatí.  Špeciálne v hyperbolickej rovine existuje takých priamok viac, napr_. l1 ,l2.

No a teraz úloha z názvu tohoto príspevku. Zostrojte v takejto hyperbolickej rovine ľubovoľný n-uholník, kde n je prirodzené číslo väčšie ako 2. Skúste prísť na všeobecný recept, resp odôvodniť či to vôbec ide.

Úloha sa dá formulovať v reči euklidovskej geometrie. Treba zostrojiť n kružníc, ktoré sa s kružnicou k pretínajú pod pravým uhlom. Ďalej treba nájsť cyklický zoznam týchto kružníc, v ktorom sa každé dve susedné kružnice budú pretínať pod pravým uhlom v kruhu K.

Dovolím si reprodukovať známu baladu, vzhľadom na to, že tvrdenie budem najbližšie potrebovať na prednáške. Takže na začiatok tóny svitu luny (od Debussyho pre pamätníkov) a nedeľná chvíľka poézie môže začať.

Heinrich von Boole-Karajan

Balada o vete Rolleovej

Túto vetu – závažnú, no krátku
nechal nám pán Rolle na pamiatku.
Každému z vás iste cestu skríži
(Neubrunn, Vencko: skriptá z analýzy).
V tej vete je skrytá vôňa kvetov.
Dovoľte mi zblížiť vás s tou vetou.

Predpoklady – tie su vskutku malé:
spojitosť na celom intervale
no a vnútri, vlastnosť to nie nová
funkciu f možno derivovať.
Na okrajoch potom už len stačí
ak sa “f(a)” “f(b)” rovnať ráči.

Keď už spĺňa tieto predpoklady,
funkcia f máva veľké klady
kdesi v (a,b) bod c sa už kľuje
f ` sa v céčku vynuluje.

Snáď stratíme ešte dve-tri slová
o tom, ako vetu dokazovať:
ak f žije medzi konštantami
urobte si, prosím, dôkaz sami.
No a ak je nekonštantne pestré
celkom iste nadobúda extrém.
Zvyšok úvah, nie je ich tak veľa
nechame na prácu čitateľa.

Je to iste pocta poézie,
že pán Rolle oddnes v básňach žije.
Zato, prosím, priateľ slovesnosti
neuberaj vetám na presnosti.
To, čo básnik do obrazov snuje
matematik presne sformuluje.

(Doplnené a opravené: autorom balady je Ivan Kupka.)

Čítal som nedávno článok o vynikajúcom geometrovi, nositeľovi viacerých ocenení – Michailovi Gromovovi. V tomto roku obdržal Abelovu cenu. Jeho postreh o  poznaní a jeho ďalšom šírení sa mi zdá veľmi trefný. Kontrastuje s prístupom skupiny známej ako Nicolas Bourbaki, ktorá vyrástla pred a najmä po druhej svetovej vojne a stavala na formálnosti. Zrejme treba oboje. MG píše:

…this common and unfortunate fact of the lack of an adequate presentation of basic ideas and motivations of almost any mathematical theory is, probably, due to the binary nature of mathematical perception: either you have no inkling of an idea or, once you have understood it, this very idea appears so embarrassingly obvious that you feel reluctant to say it aloud; moreover, once your mind switches from the state of darkness to the light, all memory of the dark state is erased and it becomes impossible to conceive the existence of another mind for which the idea appears nonobvious...

Viac pozri v článkoch Marcela Bergera, Encounter with a Geometer Part I, Part II, Notices of AMS 47, 2000.

Nech je trojuholník. Ktorý bod  v jeho vnútri minimalizuje ? Ako je to v štvorstene?

Po dlhšom čase som sa opäť stretol s hlavolamom o pútnikovi. Je z planéty, ktorá je guľatá, ale na rozdiel od Zeme, sa vie pútnik pohybovať po celom jej povrchu. Pútnik vyrazí zo svojho domu  na juh 1 km, potom na východ 1 km a na sever 1km a ocitne sa doma. Kde je jeho domov? Prezradím, že riešenie nie je jediné.

Včera som obedoval s kolegom Danom Ševčovičom, ktorý spomínal, že videl, ako sa oválne podnosy v našej jedálni prepadli na stojane, kam ich odovzdávame. To ho doviedlo na nasledujúcu úlohu, o ktorej sme sa chvíľu zhovárali.

Majme elipsu v euklidovskej rovine. Treba ukázať, že keď ju “vtesnáme” medzi ľubovoľné dve rovnobežky p,q (t.j. obe priamky sú oporné k elipse a tá je v páse medzi nimi), tak vzdialenosť týchto rovnobežiek d nie je menšia ako dĺžka vedľajšej osi.

Dá sa samozrejme ukázať viac o tejto vzdialenosti. Čo ešte by ste vedeli? Dodatok k tejto úlohe: pozrieť sa na analogickú situáciu (s rovnobežkami, nie “vtesnaním”) v prípade hyperboly a paraboly.

Toto je Pythagorova veta $c^2 = a^2+b^2$. A tu je $\int \cos x dx = \sin x + c$.

<script src='http://www.sccg.sk/~chalmo/LaTeXMathML.js' type='text/javascript'>
&lt/script&gt